DIY Video Hosting Server

Mon Feb 15 2021

Two years ago, I created a video streaming server from scratch in Node; looking back, I realized that I must have had way too much free time. I wanted something that I could use to embed videos in websites and aggregate all of my public videos. In the end, I created a lightweight node application with an administration interface, API tokens, and the ability to stream videos. Now, I can embed videos in my blog like this:

Read More »

GitHub Graphs Project

Wed Feb 20 2019

Shortly after working on my Steam Friends Graph ,I had the idea of extending the project to include the GitHub network. I used BrickHack V as the opportunity to work on this project with my friends. Rather than simply use the code that was used in the Steam friends graph, the architecture was completely revamped to reflect both the differences between the Steam and GitHub networks and my improved web development skills.

1 Project Overview

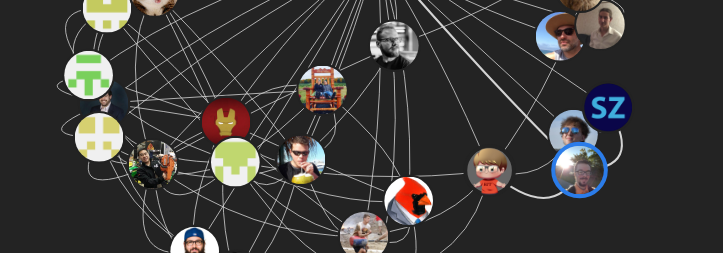
We created an interactive website which allows you to make graphs based on the Github network. Currently the site generates three types of graphs– the most popular and entertaining of which is the friends graph. The friends graph helps you visualize clusters of friends/collaborators on GitHub. Similar to the Steam Friends Project, I hope that this project will make people more interested in learning about big data. The visual aspect of this website makes learning about topics such as clustering and graph databases more intuitive.

1.1 Friends View

Read More »

Steam Friends Graph

Tue Jun 26 2018

1 Links

2 Project Description

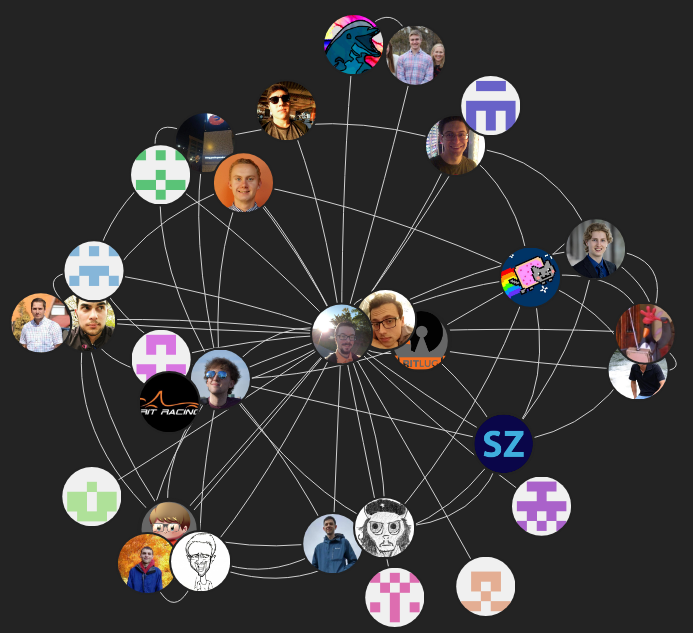
This project utilizes the steam API and graph databases to create friend graphs for clients in a web browser. Currently there are two types of graphs available: - Friends of Friends Graph: This graph displays all the steam friends of a single person and all their friend’s friends. - Common Friends Graph: This graph will only display your friends; however, it will draw edges between your friends’ if they are friends with each other.

3 Motivation

Read More »

Musical Floppy Drive Build Log

Tue Mar 13 2018

It is fun to find an interesting use for old technology. Being someone who has tons of old floppy drives and loves music, I decided to turn my old floppy drives into an orchestra. I’m not sure where I first learned about musical floppy drives, however, there are thousands of videos on YouTube.

This project first started over a year ago when I connected two floppy drives to a Raspberry Pi to play the Star Wars theme.

Read More »