My Wall Mounted Raspberry Pi Homelab

Sun Mar 01 2026

Welcome to my descent into homelabbing. With the rising cost of cloud hosting, and my DigitalOcean droplets crashing more frequently due to increased load, I decided to start self hosting more of my public facing personal projects. Most posts that I see on Reddit or Youtube regarding homelabbing tend to show off server racks filled with beefy and expensive enterprise grade equipment. This post aims to share my low-cost approach to homelabbing which uses inexpensive Raspberry PIs. I want to show that you can do really cool stuff while ‘saving’ money in the long run.

Before I started this project, I had two Raspberry PIs haphazardly perched on-top of my stereo. One of the PIs ran Pi-hole and Caddy, the other PI ran several python websites written using FastAPI. To run more stuff locally, I wanted to get another Raspberry Pi to run a firewall on OpenWRT and another Raspberry Pi to run some of my websites in Docker containers. My current arrangement of PIs wasn’t very “elegant”, so I decided to mount everything on a pegboard.

Read More »

The Data Spotify Collected On Me Over Ten Years

Sun Jan 18 2026

After using spotify for ten years, I decided to make a GDPR request and retrieve all the data that Spotify had collected on me. I intended to make a light hearted blog post that just visualized some data like a: “Spotify Wrapped but for 10 years”… After looking at the extensive amount of data that Spotify collected on me, I was a bit taken aback and decided to ditch Spotify. Recently it has become a trend to criticize Spotify for their usage of AI music and the low dividends they pay to creators– despite being the most expensive music streaming service on the market. This post is not going to add to those loud noises that are already criticizing Spotify’s business practices. This post, is going to look at Spotify’s extensive data collection and analyze my music listening habits to make an objective cost base analysis on if I would have been better off purchasing music instead of streaming from Spotify.

1 Downloading the Data

Under GDPR law, Spotify is legally obligated to provide you with all the personal data that they have stored on you. When you request your Spotify data, they offer the data export in three segments:

• Account Data
• Technical Log
• Extended Streaming History

Read More »

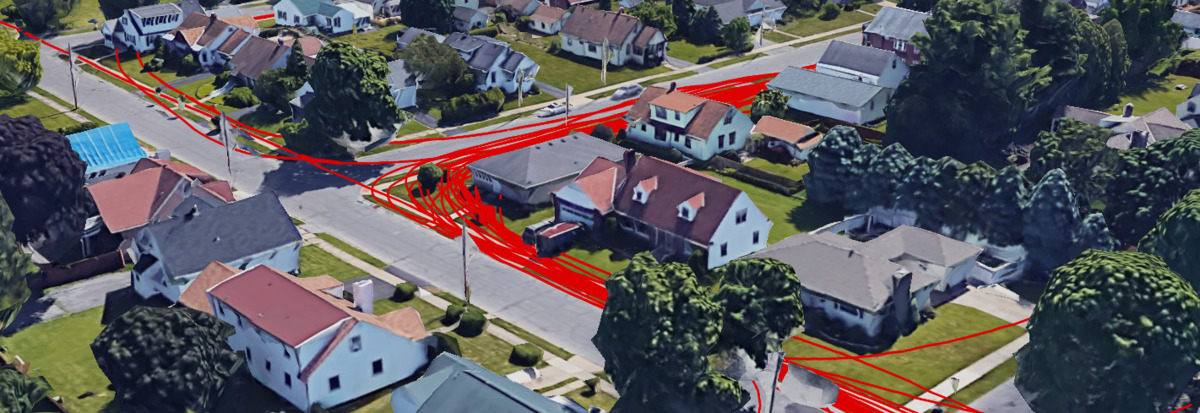
Visualizing Fitbit GPS Data

Sat May 01 2021

This post looks at how you can aggregate and visualize Fitbit GPS data since there is no built-in functionality to do this on the Fitbit website. Before you read this post, check out my two other posts on using Fitbit data:

• A Closer Look at Fitbit Data
• Graphing my Life with Matplotlib

1 Getting the Data

There are two options that we can use to fetch data from Fitbit:

• Fitbit’s Data Export Tool
• Fitbit’s API

1.1 Exporting from the Website

Read More »

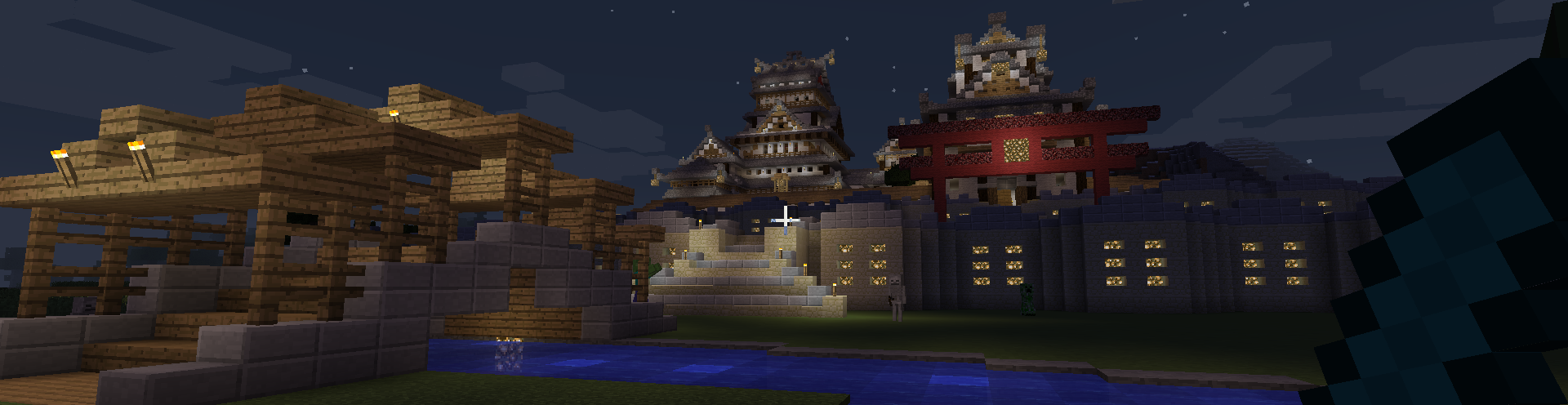
Running a Minecraft Server With Docker

Sun Feb 28 2021

Close your eyes for one moment and imagine that everything you host runs in docker containers. You no longer need to battle system dependencies, and configurations are more manageable; it is now easier to backup and transfer your applications.

In my quest to dockerize everything, I am now dockerizing my Minecraft server. Minecraft is a relatively simple application to host since it is just a single Java application that you need to run. To put this in Docker, we need to declare a Java Docker image that launches our Minecraft server.

FROM openjdk:8u232

WORKDIR /root/minecraft

CMD java -Xmx2048M -jar spigot-1.10.jar -o true

Read More »

DIY Video Hosting Server

Mon Feb 15 2021

Two years ago, I created a video streaming server from scratch in Node; looking back, I realized that I must have had way too much free time. I wanted something that I could use to embed videos in websites and aggregate all of my public videos. In the end, I created a lightweight node application with an administration interface, API tokens, and the ability to stream videos. Now, I can embed videos in my blog like this:

Read More »