Time Spent In Steam Games
Mon Jul 20 2020
Last week I scrapped a bunch of data from the Steam API using my Steam Graph Project. This project captures steam users, their friends, and the games that they own. Using the Janus-Graph traversal object, I use the Gremlin graph query language to pull this data. Since I am storing the hours played in a game as a property on the relationship between a player and a game node, I had to make a “join” statement to get the hours property with the game information in a single query.
Object o = graph.con.getTraversal()
.V()
.hasLabel(Game.KEY_DB)
.match(
__.as("c").values(Game.KEY_STEAM_GAME_ID).as("gameID"),
__.as("c").values(Game.KEY_GAME_NAME).as("gameName"),
__.as("c").inE(Game.KEY_RELATIONSHIP).values(Game.KEY_PLAY_TIME).as("time")
).select("gameID", "time", "gameName").toList();
WrappedFileWriter.writeToFile(new Gson().toJson(o).toLowerCase(), "games.json");Using the game indexing property on the players, I noted that I only ended up wholly indexing the games of 481 players after 8 hours.
graph.con.getTraversal()
.V()
.hasLabel(SteamGraph.KEY_PLAYER)
.has(SteamGraph.KEY_CRAWLED_GAME_STATUS, 1)
.count().next()We now transition to Python and Matlptlib to visualize the data exported from our JanusGraph Query as a JSON object. The dependencies for this notebook can get installed using pip.
!pip install pandas
!pip install matplotlib Collecting pandas
Downloading pandas-1.0.5-cp38-cp38-manylinux1_x86_64.whl (10.0 MB)
[K |████████████████████████████████| 10.0 MB 4.3 MB/s eta 0:00:01
[?25hCollecting pytz>=2017.2
Downloading pytz-2020.1-py2.py3-none-any.whl (510 kB)
[K |████████████████████████████████| 510 kB 2.9 MB/s eta 0:00:01
[?25hRequirement already satisfied: numpy>=1.13.3 in /home/jeff/Documents/python/ml/lib/python3.8/site-packages (from pandas) (1.18.5)
Requirement already satisfied: python-dateutil>=2.6.1 in /home/jeff/Documents/python/ml/lib/python3.8/site-packages (from pandas) (2.8.1)
Requirement already satisfied: six>=1.5 in /home/jeff/Documents/python/ml/lib/python3.8/site-packages (from python-dateutil>=2.6.1->pandas) (1.15.0)
Installing collected packages: pytz, pandas
Successfully installed pandas-1.0.5 pytz-2020.1The first thing we are doing is importing our JSON data as a pandas data frame. Pandas is an open-source data analysis and manipulation tool. I enjoy pandas because it has native integration with matplotlib and supports operations like aggregations and groupings.
import matplotlib.pyplot as plt
import pandas as pd
games_df = pd.read_json('games.json')
games_df| gameid | time | gamename | |
|---|---|---|---|
| 0 | 210770 | 243 | sanctum 2 |
| 1 | 210770 | 31 | sanctum 2 |
| 2 | 210770 | 276 | sanctum 2 |
| 3 | 210770 | 147 | sanctum 2 |
| 4 | 210770 | 52 | sanctum 2 |
| ... | ... | ... | ... |
| 36212 | 9800 | 9 | death to spies |
| 36213 | 445220 | 0 | avorion |
| 36214 | 445220 | 25509 | avorion |
| 36215 | 445220 | 763 | avorion |
| 36216 | 445220 | 3175 | avorion |
36217 rows × 3 columns
Using the built-in matplotlib wrapper function, we can graph a histogram of the number of hours played in a game.
ax = games_df.hist(column='time', bins=20, range=(0, 4000))
ax=ax[0][0]
ax.set_title("Game Play Distribution")
ax.set_xlabel("Minutes Played")
ax.set_ylabel("Frequency")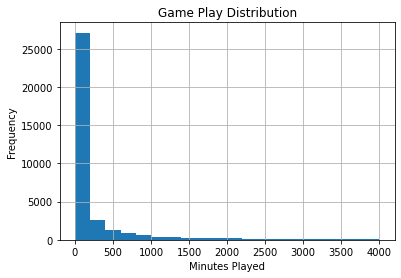
Notice that the vast majority of the games are rarely ever played, however, it is skewed to the right with a lot of outliers. We can change the scale to make it easier to view using the range parameter.
ax = games_df.hist(column='time', bins=20, range=(0, 100))
ax=ax[0][0]
ax.set_title("Game Play Distribution")
ax.set_xlabel("Minutes Played")
ax.set_ylabel("Frequency")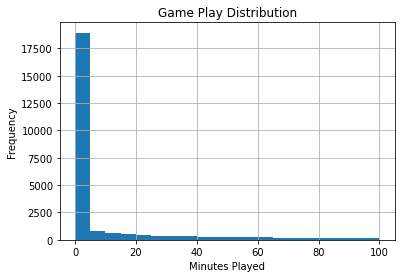
If we remove games that have never been played, the distribution looks more reasonable.
ax = games_df.hist(column='time', bins=20, range=(2, 100))
ax=ax[0][0]
ax.set_title("Game Play Distribution")
ax.set_xlabel("Minutes Played")
ax.set_ylabel("Frequency")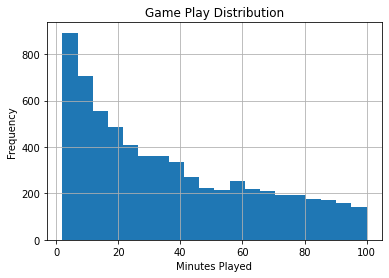
Although histograms are useful, viewing the CDF is often more helpful since it is easier to extract numerical information.
ax = games_df.hist(column='time',density=True, range=(0, 2000), histtype='step',cumulative=True)
ax=ax[0][0]
ax.set_title("Game Play Distribution")
ax.set_xlabel("Minutes Played")
ax.set_ylabel("Frequency")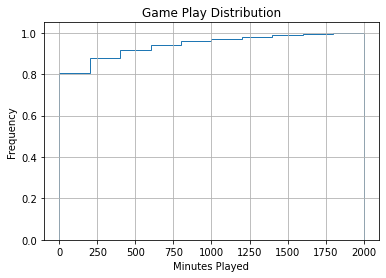
According to this graph, about 80% of people on steam who own a game, play it under 4 hours. Nearly half of all downloaded or purchased steam games go un-played. This data is a neat example of the legendary 80/20 principle – aka the Pareto principle. The Pareto principle states that roughly 80% of the effects come from 20% of the causes. IE: 20% of software bugs result in 80% of debugging time.
As mentioned earlier, the time in owned game distribution is heavily skewed to the right.
ax = plt.gca()
ax.set_title('Game Play Distribution')
ax.boxplot(games_df['time'], vert=False,manage_ticks=False, notch=True)
plt.xlabel("Game Play in Minutes")
ax.set_yticks([])
plt.show()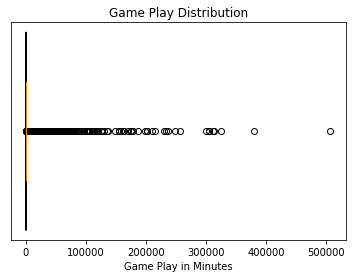
When zooming in on the distribution, we see that nearly half of all the purchased games go un-opened.
ax = plt.gca()
ax.set_title('Game Play Distribution')
ax.boxplot(games_df['time']/60, vert=False,manage_ticks=False, notch=True)
plt.xlabel("Game Play in Hours")
ax.set_yticks([])
ax.set_xlim([0, 10])
plt.show()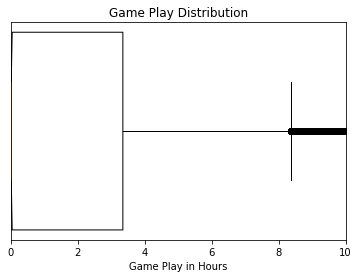
Viewing the aggregate pool of hours in particular game data is insightful; however, comparing different games against each other is more interesting. In pandas, after we create a grouping on a column, we can aggregate it into metrics such as max, min, mean, etc. I am also sorting the data I get by count since we are more interested in “popular” games.
stats_df = (games_df.groupby("gamename")
.agg({'time': ['count', "min", 'max', 'mean']})
.sort_values(by=('time', 'count')))
stats_df| time | ||||
|---|---|---|---|---|
| count | min | max | mean | |
| gamename | ||||
| 龙魂时刻 | 1 | 14 | 14 | 14.000000 |
| gryphon knight epic | 1 | 0 | 0 | 0.000000 |
| growing pains | 1 | 0 | 0 | 0.000000 |
| shoppy mart: steam edition | 1 | 0 | 0 | 0.000000 |
| ground pounders | 1 | 0 | 0 | 0.000000 |
| ... | ... | ... | ... | ... |
| payday 2 | 102 | 0 | 84023 | 5115.813725 |
| team fortress 2 | 105 | 7 | 304090 | 25291.180952 |
| unturned | 107 | 0 | 16974 | 1339.757009 |
| garry's mod | 121 | 0 | 311103 | 20890.314050 |
| counter-strike: global offensive | 129 | 0 | 506638 | 46356.209302 |
9235 rows × 4 columns
To prevent one-off esoteric games that I don’t have a lot of data for, throwing off metrics, I am disregarding any games that I have less than ten values for.
stats_df = stats_df[stats_df[('time', 'count')] > 10]
stats_df| time | ||||
|---|---|---|---|---|
| count | min | max | mean | |
| gamename | ||||
| serious sam hd: the second encounter | 11 | 0 | 329 | 57.909091 |
| grim fandango remastered | 11 | 0 | 248 | 35.000000 |
| evga precision x1 | 11 | 0 | 21766 | 2498.181818 |
| f.e.a.r. 2: project origin | 11 | 0 | 292 | 43.272727 |
| transistor | 11 | 0 | 972 | 298.727273 |
| ... | ... | ... | ... | ... |
| payday 2 | 102 | 0 | 84023 | 5115.813725 |
| team fortress 2 | 105 | 7 | 304090 | 25291.180952 |
| unturned | 107 | 0 | 16974 | 1339.757009 |
| garry's mod | 121 | 0 | 311103 | 20890.314050 |
| counter-strike: global offensive | 129 | 0 | 506638 | 46356.209302 |
701 rows × 4 columns
We see that the average, the playtime per player per game, is about 5 hours. However, as noted before, most purchased games go un-played.
ax = plt.gca()
ax.set_title('Game Play Distribution')
ax.boxplot(stats_df[('time', 'mean')]/60, vert=False,manage_ticks=False, notch=True)
plt.xlabel("Mean Game Play in Hours")
ax.set_xlim([0, 40])
ax.set_yticks([])
plt.show()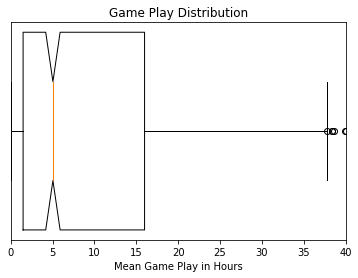
I had a hunch that more popular games got played more; however, this dataset is still too small the verify this hunch.
stats_df.plot.scatter(x=('time', 'count'), y=('time', 'mean'))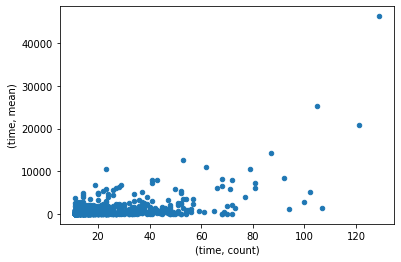
We can create a new filtered data frame that only contains the result of a single game to graph it. cc_df = games_df[games_df['gamename'] == "counter-strike: global offensive"]
cc_df| gameid | time | gamename | |
|---|---|---|---|
| 13196 | 730 | 742 | counter-strike: global offensive |
| 13197 | 730 | 16019 | counter-strike: global offensive |
| 13198 | 730 | 1781 | counter-strike: global offensive |
| 13199 | 730 | 0 | counter-strike: global offensive |
| 13200 | 730 | 0 | counter-strike: global offensive |
| ... | ... | ... | ... |
| 13320 | 730 | 3867 | counter-strike: global offensive |
| 13321 | 730 | 174176 | counter-strike: global offensive |
| 13322 | 730 | 186988 | counter-strike: global offensive |
| 13323 | 730 | 103341 | counter-strike: global offensive |
| 13324 | 730 | 10483 | counter-strike: global offensive |
129 rows × 3 columns
It is shocking how many hours certain people play in Counter-Strike. The highest number in the dataset was 8,444 hours or 352 days!
ax = plt.gca()
ax.set_title('Game Play Distribution for Counter-Strike')
ax.boxplot(cc_df['time']/60, vert=False,manage_ticks=False, notch=True)
plt.xlabel("Game Play in Hours")
ax.set_yticks([])
plt.show()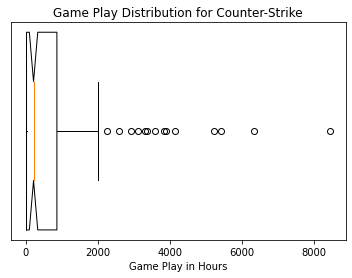
Viewing the distribution for a different game like Unturned, yields a vastly different distribution than Counter-Strike. I believe the key difference is that Counter-Strike gets played competitively, where Unturned is a more leisurely game. Competitive gamers likely skew the distribution of Counter-Strike to be very high.
u_df = games_df[games_df['gamename'] == "unturned"]
u_df| gameid | time | gamename | |
|---|---|---|---|
| 167 | 304930 | 140 | unturned |
| 168 | 304930 | 723 | unturned |
| 169 | 304930 | 1002 | unturned |
| 170 | 304930 | 1002 | unturned |
| 171 | 304930 | 0 | unturned |
| ... | ... | ... | ... |
| 269 | 304930 | 97 | unturned |
| 270 | 304930 | 768 | unturned |
| 271 | 304930 | 1570 | unturned |
| 272 | 304930 | 23 | unturned |
| 273 | 304930 | 115 | unturned |
107 rows × 3 columns
ax = plt.gca()
ax.set_title('Game Play Distribution for Unturned')
ax.boxplot(u_df['time']/60, vert=False,manage_ticks=False, notch=True)
plt.xlabel("Game Play in Hours")
ax.set_yticks([])
plt.show()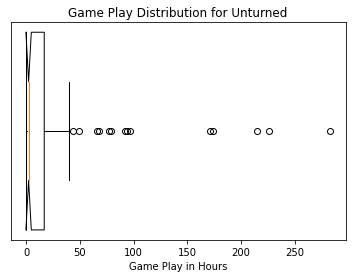
Next, I made a data frame just containing the raw data points of games that had an aggregate count of over 80. For the crawl sample size that I did, having a count of 80 would make the game “popular.” Since we only have 485 players indexed, having over 80 entries implies that over 17% of people indexed had the game. It is easy to verify that the games returned were very popular by glancing at the results.
df1 = games_df[games_df['gamename'].map(games_df['gamename'].value_counts()) > 80]
df1['time'] = df1['time']/60
df1| gameid | time | gamename | |
|---|---|---|---|
| 167 | 304930 | 2.333333 | unturned |
| 168 | 304930 | 12.050000 | unturned |
| 169 | 304930 | 16.700000 | unturned |
| 170 | 304930 | 16.700000 | unturned |
| 171 | 304930 | 0.000000 | unturned |
| ... | ... | ... | ... |
| 22682 | 578080 | 51.883333 | playerunknown's battlegrounds |
| 22683 | 578080 | 47.616667 | playerunknown's battlegrounds |
| 22684 | 578080 | 30.650000 | playerunknown's battlegrounds |
| 22685 | 578080 | 170.083333 | playerunknown's battlegrounds |
| 22686 | 578080 | 399.950000 | playerunknown's battlegrounds |
1099 rows × 3 columns
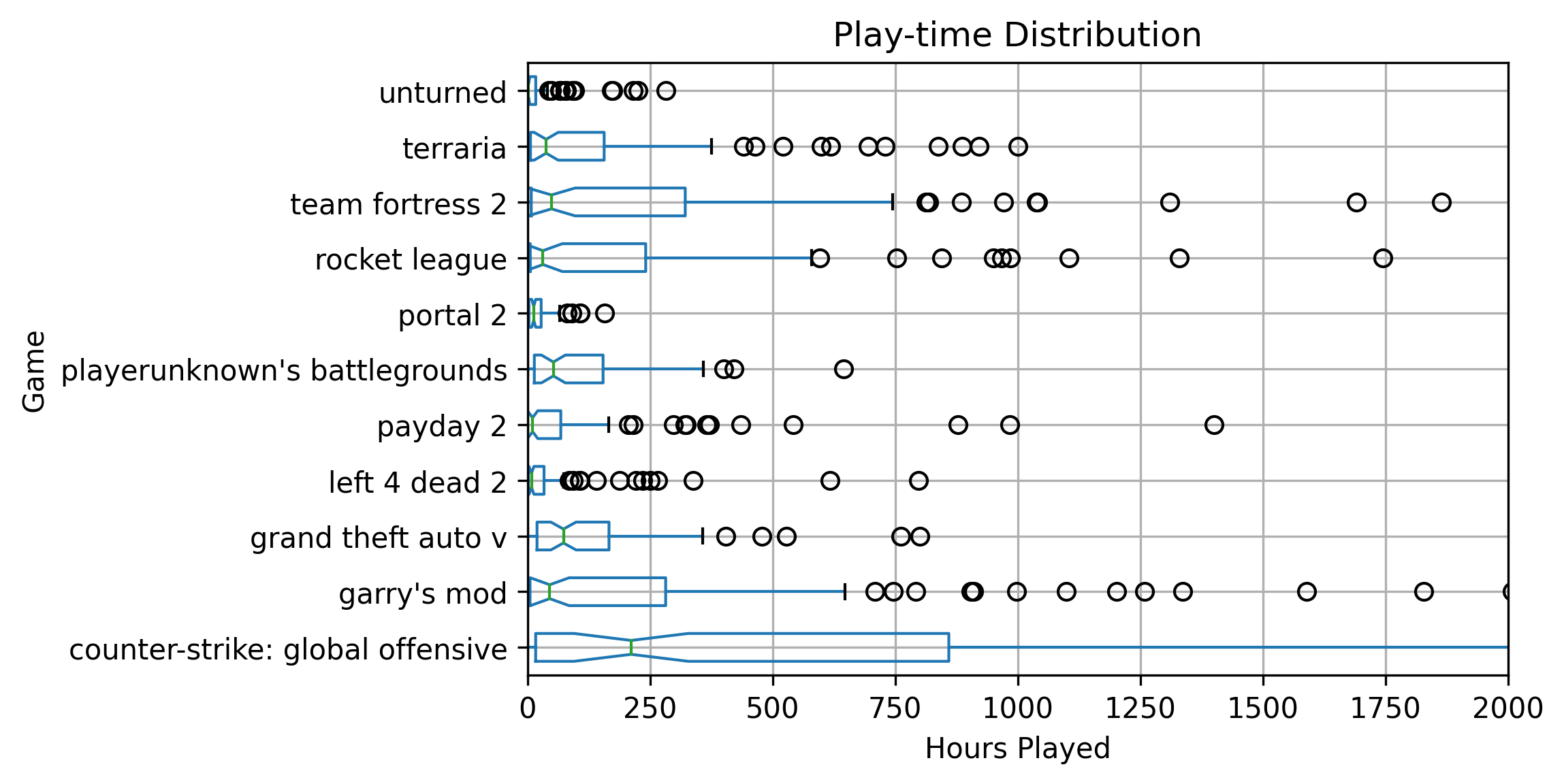
ax = df1.boxplot(column=["time"], by='gamename', notch=True, vert=False)
fig = ax.get_figure()
fig.suptitle('')
ax.set_title('Play-time Distribution')
plt.xlabel("Hours Played")
ax.set_xlim([0, 2000])
plt.ylabel("Game")
plt.savefig("playTimes.png", dpi=300, bbox_inches = "tight")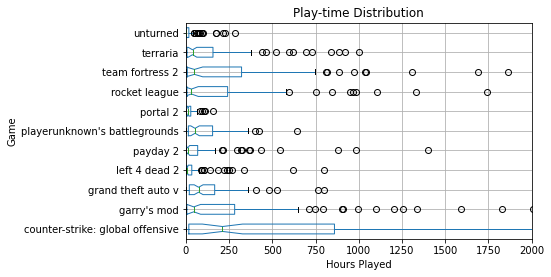
Overall it is fascinating to see how the distributions for different games vary. In the future, I will re-run some of these analytics with even more data and possibly put them on my website as an interactive graph.
Recent Posts
Visualizing Fitbit GPS DataRunning a Minecraft Server With Docker
DIY Video Hosting Server
Running Scala Code in Docker
Quadtree Animations with Matplotlib
2020 in Review
Segmenting Images With Quadtrees
Implementing a Quadtree in Python
Parallel Java Performance Overview
Pandoc Syntax Highlighting With Prism