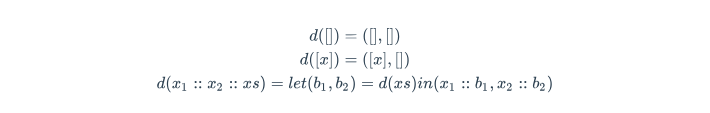
Sorting Algorithms
Sat Dec 15 2018
1 Insertion Sort
Selection sort although not very efficient is often used when the arrays you are sorting are very small. Another benefit of insertion sort is that it is very easy to program. Essentially, this algorithm has a sorted section which slowly grows as it pull in new elements to their sorted position.
1.1 Functional Notation
\[ s([]) = []\\ s(x::xs) = i(x, s(xs)) \]
\[ i(x, []) = [x]\\ i(x,y::ys) = x::y::ys, if x \leq y\\ i(x,y::yx) = y::i(x, ys) otherwise \]
If you are not familiar with functional programming, this way of writing insertion sort may scare you. Essentially the ‘s’ stands for sort and the ‘i’ stands for insert. For the sort section you are taking off the first element and inserting it into the rest of the sorted array. For the insert section you are placing the element in its sorted position.
1.2 Imperative Notation
def insertionSort(alist):
for index in range(1,len(alist)):
currentvalue = alist[index]
position = index
while position > 0 and alist[position-1] > currentvalue:
alist[position] = alist[position-1]
position = position-1
alist[position] = currentvalue
return alistThis notation will make python programmers feel a lot more comfortable.
2 Merge Sort
Merge sort is a classic example of a divide and conquer algorithm. Each iteration, the problem is cut in half making sorting it easier. Once you have your array divided into sorted sections, it is easy to combine into a larger sorted array.
2.1 Functional Notation
\[ d([]) = ([],[])\\ d([x]) = ([x],[])\\ d(x_1::x_2::xs) = let (b_1, b_2) = d(xs) in (x_1::b_1, x_2::b_2)\\ \]
\[ mSort([]) = []\\ mSort([x]) = [x]\\ mSort(xs) = let(b_1, b_2) = d(xs) in mSort(b_1) combine mSort(b_2)\\ \]
2.2 Python Implementation
def merge_sort(a):
if len(a) < 2:
return a
l = a[0:len(a)//2]
r = a[len(a)//2:]
return merge(merge_sort(l), merge_sort(r))
def merge(a, b):
out = []
i = 0
j = 0
while i < len(a) or j < len(b):
if i >= len(a):
out.append(b[j])
j += 1
elif j >= len(b):
out.append(a[i])
i += 1
else:
if a[i] <= b[j]:
out.append(a[i])
i += 1
else:
out.append(b[j])
j += 1
return out3 Quick Sort
This sorting algorithm asymptotically is the same as merge sort: \(O(nlog(n))\). However, in practice this algorithm is actually faster than merge sort due to constant factors. The general premise of this algorithm is that each iteration you will divide your array into three sections : less, equal, greater. The items in each section are based on a random element in the array. You will continue this process until you get every element by itself which makes it trivial to sort.
3.1 Functional Notation
\[ qSort([]) = []\\ qSort(x::xs) = qSort([y \in xs | y < x]) + [y \in x:xs | y = x] + qSort([y \in xs | y > x])\\ \]
This functional notation heavily uses the notion of array comprehensions.
3.2 Memory Greedy Solution
def quickSortNormal(data):
"""
This is the traditional implementation of quick sort
where there are two recursive calls.
"""
if len(data) == 0:
return []
else:
less, equal, greater = partition(data)
return quickSortNormal(less) + equal + quickSortNormal(greater)3.3 Accumulation Solution
def quick_sort_accumulation(data, a):
"""
Implementation of quickSort which forces tail recursion
by wrapping the second recursive in the tail positioned
recursive call and added an accumulation variable.
"""
if len(data) == 0:
return a
less, equal, greater = partition(data)
return quick_sort_accumulation(less,
equal + quick_sort_accumulation(greater, a))
def quicksort(data):
"""
Wrapper function for quick sort accumulation.
"""
return quick_sort_accumulation(data, [])3.4 In-Place Sorting Implementation
def iterative_partition(data, left, right):
"""
Function which partitions the data into two segments,
the left which is less than the pivot and the right
which is greater than the pivot. The pivot for this
algo is the right most index. This function returns
the ending index of the pivot.
:param data: array to be sorted
:param left: left most portion of array to look at
:param right: right most portion of the array to look at
"""
x = data[right]
i = left - 1
j = left
while j < right:
if data[j] <= x:
i = i + 1
data[i], data[j] = data[j], data[i]
j = j+1
data[i + 1], data[right] = data[right], data[i + 1]
return i + 1
def iterative_quick_sort(data):
"""
In place implementation of quick sort
Wrapper function for iterative_quick_sort_helper which
initializes, left, right to be the extrema of the array.
"""
iterative_quick_sort_helper(data, 0, len(data) -1)
return data
def iterative_quick_sort_helper(data, left, right):
"""
Uses the divide and conquer algo to sort an array
:param data: array of data
:param left: left index bound for sorting
:param right: right bound for sorting
"""
if left < right:
pivot = iterative_partition(data, left, right)
iterative_quick_sort_helper(data, left, pivot -1)
iterative_quick_sort_helper(data, pivot+1, right)4 Time Complexities Overview
| Algorithm | Worst | Average | Best |
|---|---|---|---|
| Insertion | \(0(n^2)\) | \(0(n^2)\) | \(0(n^2)\) |
| Merge | \(0(nlog(n))\) | \(0(nlog(n))\) | \(0(nlog(n))\) |
| Quick | \(0(nlog(n))\) | \(0(nlog(n))\) | \(0(n^2)\) |
Recent Posts
Visualizing Fitbit GPS DataRunning a Minecraft Server With Docker
DIY Video Hosting Server
Running Scala Code in Docker
Quadtree Animations with Matplotlib
2020 in Review
Segmenting Images With Quadtrees
Implementing a Quadtree in Python
Parallel Java Performance Overview
Pandoc Syntax Highlighting With Prism