Node2vec With Steam Data

Sun Jul 26 2020

Graph algorithms!!! Working with graphs can be a great deal of fun, but sometimes we just want some cold hard vectors to do some good old-fashioned machine learning. This post looks at the famous node2vec algorithm used to quantize graph data. The example I’m giving in this blog post uses data from my recently resurrected steam graph project.

If you live under a rock, Steam is a platform where users can purchase, manage, and play games with friends. Although there is a ton of data within the Steam network, I am only interested in the graphs formed connecting users, friends, and games. My updated visualization to show a friendship network looks like this:

Read More »

Creating a Dynamic Github Profile

Sat Jul 25 2020

Over the last few weeks, Github has been making changes to its UI. I’m the most excited about the feature that enables you to “design” your profile using a readme file. This reminds me of Myspace, where everyone had creative freedom to customize their profiles. Github being a platform for developers, people are already finding innovative ways to utilize this feature.

To create one of these readme profiles, you just need to create a repository with the same name as your account, and the content you put in the base readme file will appear over your pinned repositories on your account.

Read More »

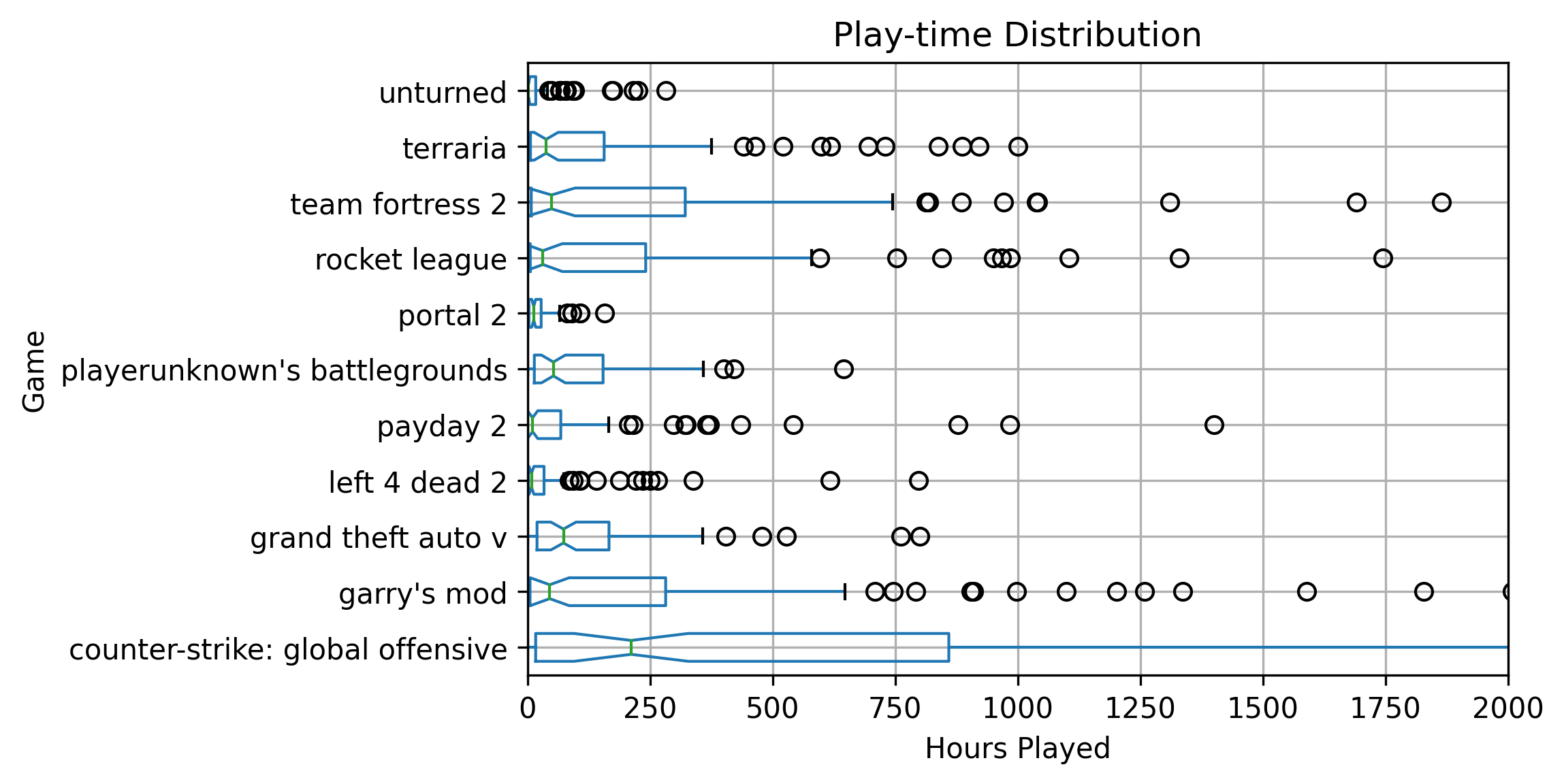
Time Spent In Steam Games

Mon Jul 20 2020

Last week I scrapped a bunch of data from the Steam API using my Steam Graph Project. This project captures steam users, their friends, and the games that they own. Using the Janus-Graph traversal object, I use the Gremlin graph query language to pull this data. Since I am storing the hours played in a game as a property on the relationship between a player and a game node, I had to make a “join” statement to get the hours property with the game information in a single query.

Object o = graph.con.getTraversal()
    .V()
    .hasLabel(Game.KEY_DB)
    .match(
            __.as("c").values(Game.KEY_STEAM_GAME_ID).as("gameID"),
            __.as("c").values(Game.KEY_GAME_NAME).as("gameName"),
            __.as("c").inE(Game.KEY_RELATIONSHIP).values(Game.KEY_PLAY_TIME).as("time")
    ).select("gameID", "time", "gameName").toList();
WrappedFileWriter.writeToFile(new Gson().toJson(o).toLowerCase(), "games.json");

Using the game indexing property on the players, I noted that I only ended up wholly indexing the games of 481 players after 8 hours.

graph.con.getTraversal()
    .V()
    .hasLabel(SteamGraph.KEY_PLAYER)
    .has(SteamGraph.KEY_CRAWLED_GAME_STATUS, 1)
    .count().next()

Read More »

Fun With Functional Java

Mon Jul 13 2020

It’s time I tell you all my un-popular opinion: Java is a fun language. Many people regard Java as a dingy old language with vanilla syntax. Please don’t fret; I am here to share the forbidden knowledge and lure you into the rabbit hole that is functional programming esque syntax in Java. And yes, this goes way beyond merely having lambda statements.

1 Ways to create a list

The plain old way of making a list would look something like this:

List<Integer> myList = new ArrayList<Integer>();
myList.add(1);
myList.add(2);
myList.add(3);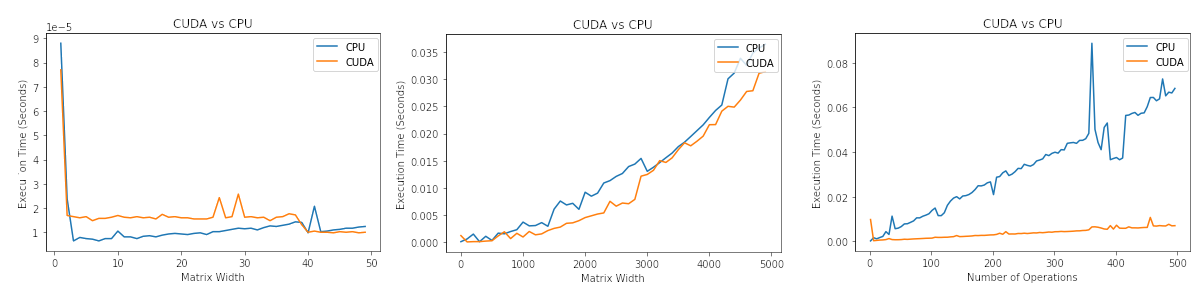

Read More »

CUDA vs CPU Performance

Fri Jul 03 2020

High-performance parallel computing is all the buzz right now, and new technologies such as CUDA make it more accessible to do GPU computing. However, it is vital to know in what scenarios GPU/CPU processing is faster. This post explores several variables that affect CUDA vs. CPU performance. The full Jupyter notebook for this blog post is posted on my GitHub.

For reference, I am using an Nvidia GTX 1060 running CUDA version 10.2 on Linux.

!nvidia-smi

    Wed Jul  1 11:16:12 2020       
    +-----------------------------------------------------------------------------+
    | NVIDIA-SMI 440.82       Driver Version: 440.82       CUDA Version: 10.2     |
    |-------------------------------+----------------------+----------------------+
    | GPU  Name        Persistence-M| Bus-Id        Disp.A | Volatile Uncorr. ECC |
    | Fan  Temp  Perf  Pwr:Usage/Cap|         Memory-Usage | GPU-Util  Compute M. |
    |===============================+======================+======================|
    |   0  GeForce GTX 1060..  Off  | 00000000:01:00.0  On |                  N/A |
    |  0%   49C    P2    26W / 120W |   2808MiB /  3016MiB |      2%      Default |
    +-------------------------------+----------------------+----------------------+
                                                                                   
    +-----------------------------------------------------------------------------+
    | Processes:                                                       GPU Memory |
    |  GPU       PID   Type   Process name                             Usage      |
    |=============================================================================|
    |    0      1972      G   /usr/libexec/Xorg                             59MiB |
    |    0      2361      G   /usr/libexec/Xorg                            280MiB |
    |    0      2485      G   /usr/bin/gnome-shell                         231MiB |
    |    0      5777      G   /usr/lib64/firefox/firefox                     2MiB |
    |    0     33033      G   /usr/lib64/firefox/firefox                     4MiB |
    |    0     37575      G   /usr/lib64/firefox/firefox                   167MiB |
    |    0     37626      G   /usr/lib64/firefox/firefox                     2MiB |
    |    0     90844      C   /home/jeff/Documents/python/ml/bin/python   1881MiB |
    +-----------------------------------------------------------------------------+

Read More »